p進数　(p-adic number)：たまの週末：SSブログ

	ブログをはじめるログイン

p進数　(p-adic number)　[科学、数学] [編集]

「シンメトリーの地図帳」に、モジュラー算術（modular arithmetic; モジュラ計算）という計算方法が出てきます。

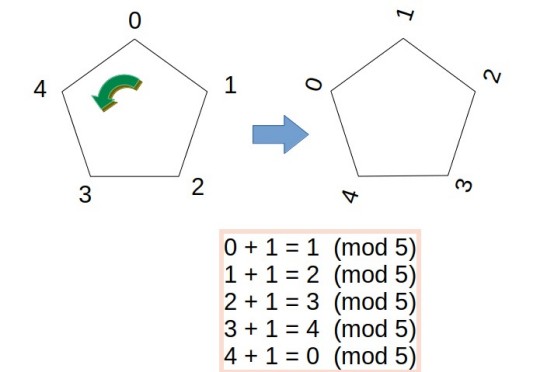
5角形の世界（「5を法とする」といいます。）を例に、足し算をしてみると
0 + 1 = 1 (mod 5)
は、普通の整数の足し算と同じですが、
4 + 1 = 0 (mod 5)
は、整数の足し算とは、違う結果になります。
時計の針を１２時から１時間すすめると、13時ではなく１時になるのと似ています。
時計算術（Clock arithmetic）とも呼ばれるようです。

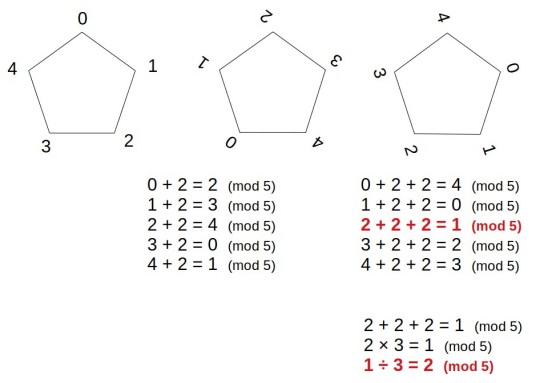
整数の世界では、足し算、引き算、掛け算の答えは、整数になりますが、割り算は、 1 ÷ 3 のように、答えが整数にならないものがありますが、モジュラ算術では、法(modules)が素数のときには、割り算の答えも必ず整数になるという便利（？）な性質があります。

５を法とするモジュラー計算では、 1 ÷ 3 = 2
になります。

数論の世界でも、p進数（p-adic number）という割り算の答えも必ず整数になる、便利な世界があります。
p進数のpは、素数を意味していて、10進数や、コンピュータのプログラミングで使われる16進数などは、p進数とは言いません。

計算機代数アプリケーションのPARI/GPでは、
n + O(p^e)
という形で、p進数を定義することができます。
eは、p進数のprecision （桁数）で、省略すると1になります。

5角形の計算の
4 + 1 = 0 (mod 5)
は、
n = 4 + O(5)
n + 1
= 0 + O(5)

1÷3 は、
n = 1 + O(5)
n / 3
= 2 + O(5)

のようになります。

p進数は、四則演算だけでなく、平方根の計算結果も整数になります。
PARI/GPのチュートリアル（https://pari.math.u-bordeaux.fr/tutorials.html）の例

569 の7進数
2 + 4*7 + 4*7^2 + 7^3 + O(7^8)
の平方根 s を求め、sの自乗と569の７進数が等しいことを確認します。

? n = 569 +O(7^8)
%1 = 2 + 4*7 + 4*7^2 + 7^3 + O(7^8)
? s = sqrt(n)
%2 = 3 + 4*7 + 7^2 + 3*7^3 + 7^4 + 5*7^5 + 2*7^6 + O(7^8)
? s^2 - n
%3 = O(7^8)

平方根の計算は、できましたが、自然対数（natural logarithm）のような、超越関数（transcendental function）は、どうでしょうか？

? s = log(n)
%4 = 6*7^2 + 4*7^4 + 3*7^5 + 3*7^6 + 3*7^7 + O(7^8)
? e = exp(s)
%5 = 1 + 6*7^2 + 7^4 + 6*7^5 + 2*7^7 + O(7^8)
? e - n
%6 = 6 + 2*7 + 7^2 + 6*7^3 + 6*7^5 + 2*7^7 + O(7^8)

自然対数の計算をした結果を指数計算しても、もとにもどりません...

p進数で、超越関数の計算をできるようにするためには、タイヒミュラー指数（Teichmüller character）という指数を導入する必要があるらしいです。

PARI/GPには、タイヒミューラ指数を求めるteichmuller関数が用意されています。　PARI/GPすごい。

? e * teichmuller(n) - n
%7 = O(7^8)

もとの数nとの差がなくなりました。

PARI/GPのチュートリアル、とってもためになるのですが、絵的に寂しい...

タイヒミュラー空間の雰囲気（？）が、わかりそうな、
The PML(Projective Measured Laminations) Visualization Project
http://homepages.math.uic.edu/~ddumas/PML/
というのがあったので、動画を作って、貼り付けときます。