晴天 [相鉄沿線]
雲一つ無い青空になりました。
横浜の最高気温29.9℃だったそうです。もうちょっとで真夏日

ビワの実、もうすぐ食べられそう。

桑の実も沢山なっていました。



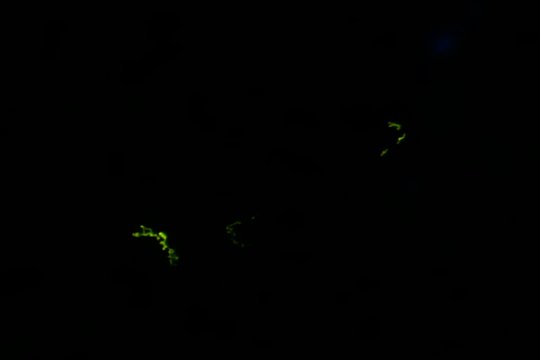
日が暮れてからも、蒸し暑いので、もしかしたらと思って、こども自然公園に行ってみたら、ホタルが飛んでいました。
横浜の最高気温29.9℃だったそうです。もうちょっとで真夏日
ビワの実、もうすぐ食べられそう。
桑の実も沢山なっていました。
日が暮れてからも、蒸し暑いので、もしかしたらと思って、こども自然公園に行ってみたら、ホタルが飛んでいました。
うみそらデッキに行きました。 [ヨコハマ]
横浜に健康診断に行った帰りに、(今更ですが)JR横浜タワーの「うみそらデッキ」に行きました。

空が広い
ビルの間から、横浜港が見えます。


久しぶりに都会に出て来たので、都会の大きな本屋さん(有隣堂です)に行ったら「抽象数学の手ざわり」という変わったタイトルの本があったので買ってみました。
岩波科学ライブラリー 抽象数学の手ざわり ピタゴラスの定理から圏論まで
https://www.iwanami.co.jp/book/b584810.html

まだ、0章(この本では自然数Nは、0から始まることにしている)の「ピタゴラスの定理から圏論まで」ぐらいしか読んでないのですが、「はじめに」には、こんなことが書いてあります。
「・・・20世紀に,物理学や生物学はそれぞれ量子力学や分子生物学の成立により,著しい変貌を遂げました.それとほぼ同時期に数学も抽象的な方向へ大きく転換しました.しかし高校までに学ぶ数学の大部分は,この転換期よりも前に完成したものです.そのため,数学でいまどんな対象について何を考えているのか,感覚がつかみにくくなっているように思います。
この隔たりを埋めたいと思ってできたのがこの本です.・・・」
そうなんですよね... 高校まで数学(受験数学)が得意だったけど、「大学の数学、全然わからない、デデキント・カットって何だよ、キットカットと違うの?...」って思った人、けっこういるんじゃないかな?(私だけ?)
この本は、そんな人たちにお薦めだと思います。
最近、「そんなの何の役に立つの、社会に出て使わない」って言うの流行っているみたいで、この本に対しても、Amazonのレビューで、「数学者の自己満足、数学者よりエンジニアの方がよっぽど数学できる」みたいな「言いがかりのような謎レビュー」がありました。(今は消されてるようです。)
最近話題の三角関数は必要だけど、現代数学は役に立たないと言う人も多いようですが、量子力学や分子生物学などに限らず、工学の分野でも、たとえばAMやFMなどのアナログ放送(アナログ変調方式)であれば、三角関数やフーリエ解析などを使って設計や解析を行うと思いますが、携帯電話の5Gのデジタル通信で使われているPolar code(これってWikipediaでは英語や中国語の説明はあるのに日本語は無いんですね)やRSA暗号やオペレーションズ・リサーチで使われる整数計画法(Integer Programming)などは、高校までの数学(受験数学)の世界にはなかった数学が必要になります。
金融の分野でも、「ブラック・ショールズ・モデルで三角関数を使うぞ」っていうのネットで見ましたが、少なくともメガバンクや大手証券会社などのセルサイドの実務では、10年以上前からブラック・ショールズ・モデルは使っていないはずです。(今どき使っていたら外資にカモられます)
高校までの数学(受験数学)と、現代の科学や工学(量子力学や分子生物学やICTなど)に必要な数学とのギャップをうまく埋めることができていないことが、デジタル化や先端技術分野で日本が世界から取り残されている原因の一つかもしれないですね。

空が広い
ビルの間から、横浜港が見えます。
久しぶりに都会に出て来たので、都会の大きな本屋さん(有隣堂です)に行ったら「抽象数学の手ざわり」という変わったタイトルの本があったので買ってみました。
岩波科学ライブラリー 抽象数学の手ざわり ピタゴラスの定理から圏論まで
https://www.iwanami.co.jp/book/b584810.html
まだ、0章(この本では自然数Nは、0から始まることにしている)の「ピタゴラスの定理から圏論まで」ぐらいしか読んでないのですが、「はじめに」には、こんなことが書いてあります。
「・・・20世紀に,物理学や生物学はそれぞれ量子力学や分子生物学の成立により,著しい変貌を遂げました.それとほぼ同時期に数学も抽象的な方向へ大きく転換しました.しかし高校までに学ぶ数学の大部分は,この転換期よりも前に完成したものです.そのため,数学でいまどんな対象について何を考えているのか,感覚がつかみにくくなっているように思います。
この隔たりを埋めたいと思ってできたのがこの本です.・・・」
そうなんですよね... 高校まで数学(受験数学)が得意だったけど、「大学の数学、全然わからない、デデキント・カットって何だよ、キットカットと違うの?...」って思った人、けっこういるんじゃないかな?(私だけ?)
この本は、そんな人たちにお薦めだと思います。
最近、「そんなの何の役に立つの、社会に出て使わない」って言うの流行っているみたいで、この本に対しても、Amazonのレビューで、「数学者の自己満足、数学者よりエンジニアの方がよっぽど数学できる」みたいな「言いがかりのような謎レビュー」がありました。(今は消されてるようです。)
最近話題の三角関数は必要だけど、現代数学は役に立たないと言う人も多いようですが、量子力学や分子生物学などに限らず、工学の分野でも、たとえばAMやFMなどのアナログ放送(アナログ変調方式)であれば、三角関数やフーリエ解析などを使って設計や解析を行うと思いますが、携帯電話の5Gのデジタル通信で使われているPolar code(これってWikipediaでは英語や中国語の説明はあるのに日本語は無いんですね)やRSA暗号やオペレーションズ・リサーチで使われる整数計画法(Integer Programming)などは、高校までの数学(受験数学)の世界にはなかった数学が必要になります。
金融の分野でも、「ブラック・ショールズ・モデルで三角関数を使うぞ」っていうのネットで見ましたが、少なくともメガバンクや大手証券会社などのセルサイドの実務では、10年以上前からブラック・ショールズ・モデルは使っていないはずです。(今どき使っていたら外資にカモられます)
高校までの数学(受験数学)と、現代の科学や工学(量子力学や分子生物学やICTなど)に必要な数学とのギャップをうまく埋めることができていないことが、デジタル化や先端技術分野で日本が世界から取り残されている原因の一つかもしれないですね。

抽象数学の手ざわり: ピタゴラスの定理から圏論まで (岩波科学ライブラリー 305)
- 作者: 斎藤 毅
- 出版社/メーカー: 岩波書店
- 発売日: 2021/07/20
- メディア: 単行本
素数の音楽を読みました。(その2) [科学、数学]
(格子: Latticeの例)
前回は、最近読んだマーカス デュ・ソートイ の「素数の音楽 (新潮文庫)」に書かれていたリーマン予想について書きましたが、この本には、インターネットで利用されているRSA(Rivest–Shamir–Adleman:発明者3人の名前)暗号の誕生や、RSA129 の解読には、4京年かかると思って懸賞金をかけたら、レンストラとマナッスによって1994年に解かれてしまった話なども書かれています。
RSA129とレンストラ博士の話は、当時のThe New York Times の記事にもなっています。(タイトルが長い)
The Assault on 114,381,625,757,888,867,669,235,779,976,146,612,010,218,296,271,242,362,562,561,842,935,706,935,245,733,897,830,597,123,563,958,705,058,989,075,147,599,290,026,879,543,541
https://www.nytimes.com/1994/03/22/science/assault.html
コンピュータの性能が高くなったことと、効率の良い計算方法が発見されたことで、暗号の強度を保つためには、桁数の多いより複雑な鍵を使わなければならなくなって、現在では2048ビット以上の長さが推奨されていますが、この先さらに効率の良いプログラムや量子コンピュータができてしまたときのために、米国国立標準技術研究所(NIST)を中心に耐量子計算機暗号(PQC: Post-quantum cryptography)という新しい暗号化の標準を決めようとしているそうです。(もうすぐ決まる)
https://csrc.nist.gov/Projects/post-quantum-cryptography
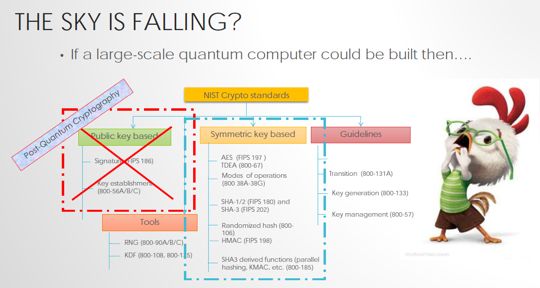
(ちょっと古い資料だけど、絵がかわいいので:https://csrc.nist.gov/CSRC/media/Projects/Post-Quantum-Cryptography/documents/asiacrypt-2017-moody-pqc.pdf
THE SHIP HAS SAILED The NIST Post-Quantum Crypto “Competition”Dustin Moody, NIST )
レンストラ博士が考えたRSAへのアタックは、レンストラ–レンストラ–ロヴァッツの格子基底縮小アルゴリズム(Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm)という計算方法を利用するもので、UCSDなどでは学部の授業でやるみたいです。(200番台なので2年生?)
https://cse.ucsd.edu/graduate/current-quarter-course-descriptions-recommended-preparation
全くヒントがない暗号文だと、パソコンでは1年かけても計算できませんが、短い文章や、文章の一部分がわかっていると、ノートパソコンでも一瞬で計算できます。
UCSDの CSE 291-I: Applied Cryptography Nadia Heninger UCSD Spring 2020 Lecture 17
https://cseweb.ucsd.edu/classes/sp20/cse291-i/lectures/17-lattices-notes.pdf
にSage Mathで計算する例があったので、自分のノートパソコンでやってみました。
---
N=random_prime(2^150)*random_prime(2^150)
message = Integer('thepasswordfortodayisswordfish' , base=35)
c=message^3%N
# 'thepasswordfortodayis’ まで分かっていてパスワードが謎の場合
a=Integer('thepasswordfortodayis000000000' ,base=35)
X=Integer('xxxxxxxxx' ,base=35)
M=matrix([[X^3,3*X^2*a,3*X*a^2,a^3-c], [0,N*X^2,0,0],[0,0,N*X,0],[0,0,0,N]])
# LLL格子基底縮小
%time
B=M.LLL()
Q=B[0][0]*x^3/X^3+B[0][1]*x^2/X^2+B[0][2]*x/X+B[0][3]
Q.roots(ring=ZZ)[0][0].str(base=35)
# CPU times: user 0 ns, sys: 0 ns, total: 0 ns
# Wall time: 3.34 µs
# 解読結果
# 'swordfish'
ちなみに、パスワードの例’swordfish'は、ハッカーが主人公の映画のタイトルで、映画の中で「最もハッキングされにくいコンピュータは何か知っているか?DECのコンピュータだ、なぜなら使っている人が少ないから」みたいな会話があって、私はDECに勤めていたので、ちょっと複雑な気持ちでした。
リーマンのゼータ関数の複素平面のプロット、英語版のWiki
https://en.wikipedia.org/wiki/Riemann_zeta_function
にかっこいいのがあったので、真似してみました。
たぶん
https://github.com/davidlowryduda/phase_mag_plot
を使っているんじゃないかな?
大きな白い花の木 [相鉄沿線]
森の中で、大きな白い花の木を見つけました。
よく見ると、大きな木にからまった白い藤の花でした。
風下に立つと、甘い香りが漂ってきます。
こども自然公園の、大きな白い花のナンジャモンジャの木
大きな白い花のホウノキ
「大きな白い花のナンジャモンジャの木」は、木が大きいけど、「大きな白い花のホウノキ」は、花が大きいのか、ホウノキが大きいのか、どちらもありそうです。
木が大きなときは、「白い花の咲く大きな木」とすればわかりやすいけど、花が大きいときは「大きな白い花の咲いている木」としても、大きな木もありそう...「白い花の大木」とか「大輪の白い花の木」のように言えばいいのかな?
英語だと、A large tree with white flowers. と A tree with large white flowers.のように区別しやすい表現をすると思うのですが、日本語は難しいですね。
「大きな栗の木」は、木が大きい、「大きな栗のなる木」は、栗が大きいような気がするけど、「大きい実のなる木」は、実が大きいのか、「実のなる木」が大きいのかよくわからない...
英語の場合は、形容詞が2つ以上の場合の順番が、OSASCOMP (Opinion, Size, Age, Shape, Color, Origin, Material, Purpose )のように決まっているけど、日本語だと「白い大きい花の木」も「大きい白い花の木」もあって、「白い大きい花の木」の方は「花が大きい」というのがわかるような木がする。じゃなくて気がする。(白いという形容詞は、木より花に使われることが多いから?)
英語は、形容詞の順番が決まっていたり、SVOのように単語の位置で、主語と述語の役割が決まったりするけど、日本語の場合は、単語の位置より助詞の役割が大きかったり、形容詞も「白い」に対して「花」「木」のような名詞が並んでいたら、たぶん木が白いんじゃなくて、花が白いんだろうとか、過去の経験や学習による判断(空気を読むとか?行間を読むとか?)が必要なので、AIの自然言語処理で、英語圏の人が作った仕組みを日本語にあてはめても、なかなかうまく行かないのかもしれないですね。
素数の音楽を読みました。 [科学、数学]
日曜日は、午前中から雨になってしまったので、マーカス デュ・ソートイ の「素数の音楽 (新潮文庫)」という本を読みました。

日本語版は2013年に発売されていて、以前から本屋さんに並んでいたので気になっていたのですが、なんで今まで読んでなかったんだろう...
素数というと、小学生か中学生のころに、「エラトステネスのふるい」という素数の見つけ方を習ったと思うのですが、この本では、無限に続く素数の見つけ方を探す話から、素数がどのように分布しているのかというリーマン予想を中心に、素数と暗号や量子力学など様々な分野との関係が書かれています。
登場人物も、リーマン、ヒルベルト、ディリクレ、ゲーデル、ラマヌジャン、ヴェイユ、コンヌなど綺羅星のような超一流の数学者たちが大勢並んでいて、物語としてとても面白いです。
この本に、綺麗な図や写真などがあったらもっと楽しいだろうな、と思いましたが、それだと本の値段が高くなってしまいますね。
それなら、自分で描いてみようということで...
リーマン予想(Riemann hypothesis)とは、リーマンゼータ関数
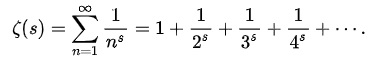
のゼロ点が、負の偶数と、実部が 1/2 の複素数に限られるという予想で1859年に提唱されてから現在まで証明されておらず、2000年には、クレイ数学研究所が100万ドルの懸賞金をかけています。
Sage Math ( https://www.sagemath.org/ )というソフトを使うと、リーマン予想で使われているゼータ関数の複素平面での様子を、complex_plot関数とzeta関数のたった2つの関数だけで表示することができます。
complex_plot(zeta, (-30,30), (-30,30))
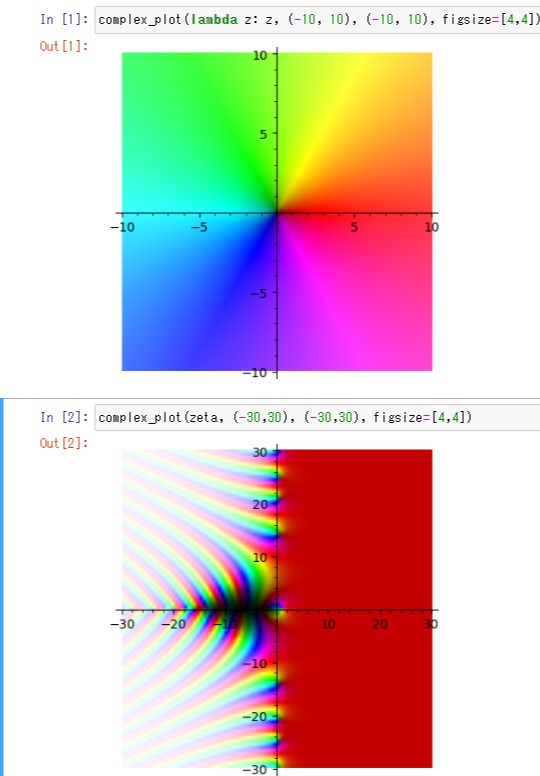
上の図のOut[1]は、カラーの凡例です。偏角0が赤、π/2が黄緑、πが水色、3/2・πが青紫になっています。
下のOut[2]のゼータ関数をカラーでマッピングした図の中で、y軸より右側(x>0)に、青や黄色がはみ出しているあたりが非自明のゼロ点になります。
zeta関数の値を、絶対値(赤)、実部(青)、虚部(緑)にして等高線図(コンター)で表示してみました。
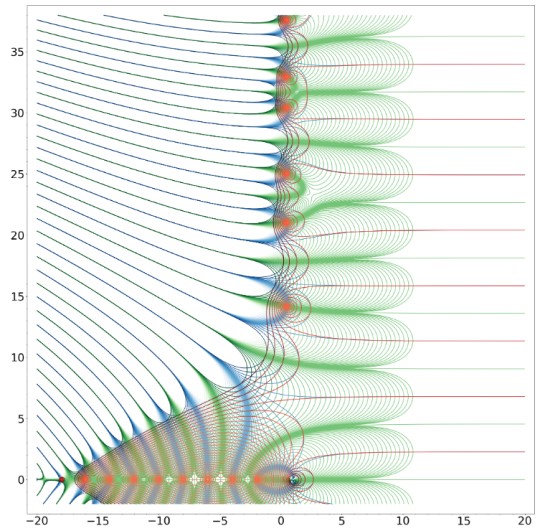
赤の線の密度が濃いところがゼロ点で、x軸上(y=0)のx=-2, -4, -6...は自明なゼロ点、x=1/2 のところで縦に並んでいる点が非自明のゼロ点になります。
x=1/2の臨界線上のゼータの値をy=0 (虚数部 0i )から200 ( 200i )まで、順番に計算した様子を動画にすると、x= -1.5 の近く( ζ(1/2 + 0i) = -1.4603545... ) からスタートして、ぐるぐる回りながら、ときどき原点Oを通ることがわかります。
再生できない場合、ダウンロードは🎥こちら
ネットで検索してみたら、こんな本も出版されていたんですね。
やっぱり綺麗な図があると、楽しそうですね。
ビジュアル リーマン予想入門 ~グラフで解き明かす素数とゼータ関数の関係 Tankobon Softcover – July 17, 2020
https://gihyo.jp/book/2020/978-4-297-11452-7

日本語版は2013年に発売されていて、以前から本屋さんに並んでいたので気になっていたのですが、なんで今まで読んでなかったんだろう...
素数というと、小学生か中学生のころに、「エラトステネスのふるい」という素数の見つけ方を習ったと思うのですが、この本では、無限に続く素数の見つけ方を探す話から、素数がどのように分布しているのかというリーマン予想を中心に、素数と暗号や量子力学など様々な分野との関係が書かれています。
登場人物も、リーマン、ヒルベルト、ディリクレ、ゲーデル、ラマヌジャン、ヴェイユ、コンヌなど綺羅星のような超一流の数学者たちが大勢並んでいて、物語としてとても面白いです。
この本に、綺麗な図や写真などがあったらもっと楽しいだろうな、と思いましたが、それだと本の値段が高くなってしまいますね。
それなら、自分で描いてみようということで...
リーマン予想(Riemann hypothesis)とは、リーマンゼータ関数
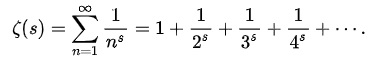
のゼロ点が、負の偶数と、実部が 1/2 の複素数に限られるという予想で1859年に提唱されてから現在まで証明されておらず、2000年には、クレイ数学研究所が100万ドルの懸賞金をかけています。
Sage Math ( https://www.sagemath.org/ )というソフトを使うと、リーマン予想で使われているゼータ関数の複素平面での様子を、complex_plot関数とzeta関数のたった2つの関数だけで表示することができます。
complex_plot(zeta, (-30,30), (-30,30))

上の図のOut[1]は、カラーの凡例です。偏角0が赤、π/2が黄緑、πが水色、3/2・πが青紫になっています。
下のOut[2]のゼータ関数をカラーでマッピングした図の中で、y軸より右側(x>0)に、青や黄色がはみ出しているあたりが非自明のゼロ点になります。
zeta関数の値を、絶対値(赤)、実部(青)、虚部(緑)にして等高線図(コンター)で表示してみました。

赤の線の密度が濃いところがゼロ点で、x軸上(y=0)のx=-2, -4, -6...は自明なゼロ点、x=1/2 のところで縦に並んでいる点が非自明のゼロ点になります。
x=1/2の臨界線上のゼータの値をy=0 (虚数部 0i )から200 ( 200i )まで、順番に計算した様子を動画にすると、x= -1.5 の近く( ζ(1/2 + 0i) = -1.4603545... ) からスタートして、ぐるぐる回りながら、ときどき原点Oを通ることがわかります。
再生できない場合、ダウンロードは🎥こちら
ネットで検索してみたら、こんな本も出版されていたんですね。
やっぱり綺麗な図があると、楽しそうですね。
ビジュアル リーマン予想入門 ~グラフで解き明かす素数とゼータ関数の関係 Tankobon Softcover – July 17, 2020
https://gihyo.jp/book/2020/978-4-297-11452-7

ビジュアル リーマン予想入門 ~グラフで解き明かす素数とゼータ関数の関係
- 作者: 木内 敬
- 出版社/メーカー: 技術評論社
- 発売日: 2020/07/17
- メディア: 単行本(ソフトカバー)




